Deriving Symmetry - Solution

Graphs of Even Functions with their Derivatives

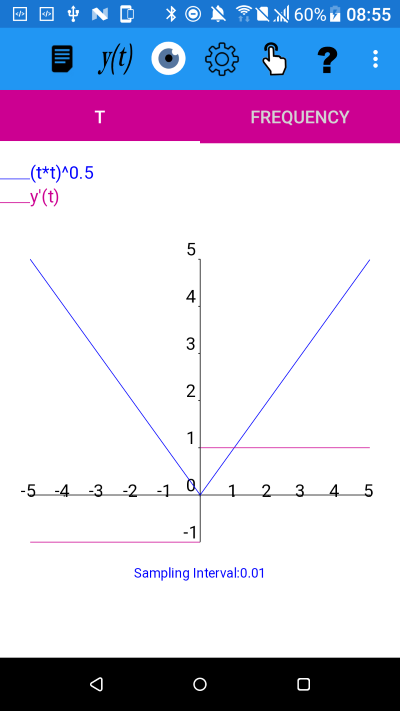
y=|t| using |t|=(t*t)^0.5

From the image it appears that the derivative is an odd function (excluding t=0) because if the derivative graph is reflected in the y axis it results in an upside down version of itself. Note that the derivative of |t| is not defined for t=0.

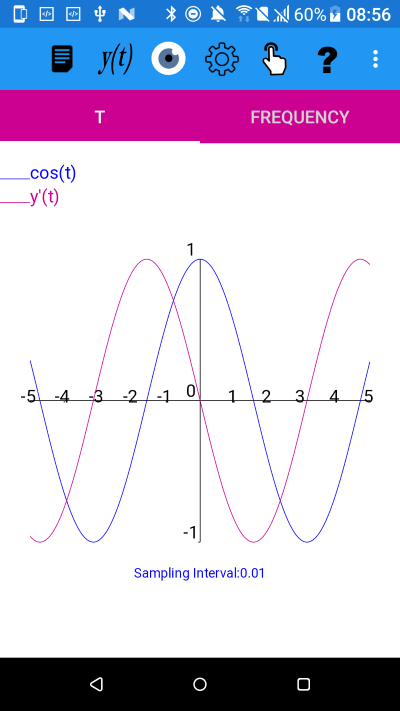
y=cos(t)

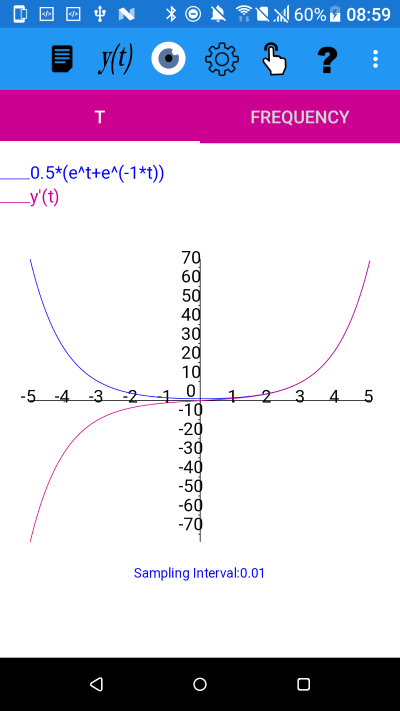
From the image it appears that the derivative is an odd function.

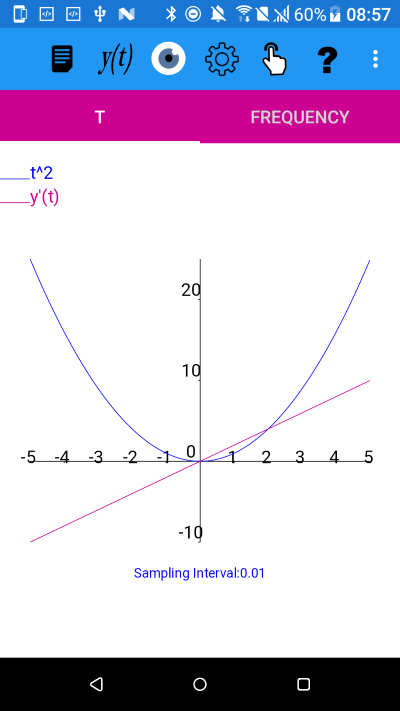
y=t^2

t squared and its derivative. t squared is an even function and its derivative is odd

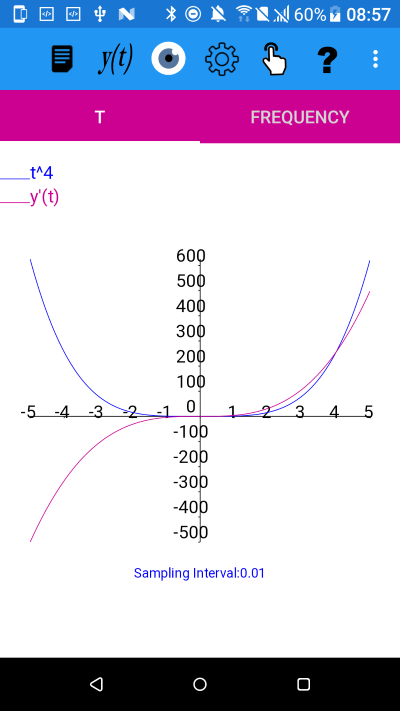
y=t^4

t to the power 4 and its derivative. t to the power 4 is an even function and its derivative is odd

y=cosh(t) using cosh(t)=0.5(e^t+e^(-1t))

cosh(t), using cosh(t)=0.5*(e^t+e^(-1*t)), and its derivative. cosh(t) is an even function and its derivative is odd

The Maclaurin series for a general function, f(t), defined around t=0 and with all its derivatives defined at t=0 is given by:

The Maclaurin series for a general function, defined around t=0 and with all its derivatives defined at t=0

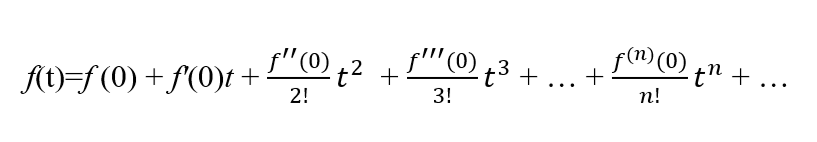
If a function is even then it will only have even powers of t in its Maclaurin series, i.e. f'(0) and f'''(0) and f⁽ⁿ⁾(0) for n odd, must all be 0.

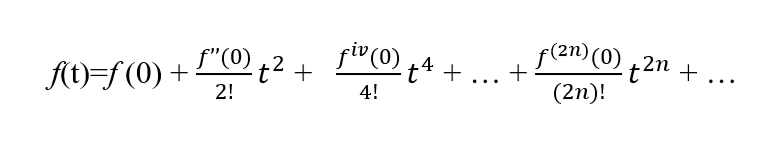
Differentiating above we get:

The power series for the derivative of an even function. We see that the power series for the derivative consists of only odd powers of t and therefore is odd

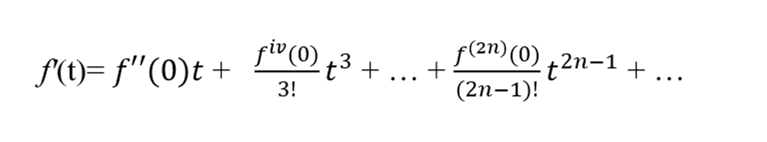
We see that the power series for the derivative consists of only odd powers of t and therefore is odd.

plotXpose app is available on Google Play and App Store

Google Play and the Google Play logo are trademarks of Google LLC.
A version will shortly be available for Windows.

plotXpose app is a companion to the book Mathematics for Electrical Engineering and Computing by Mary Attenborough, published by Newnes, 2003.