Inverse differentiation? - Solution
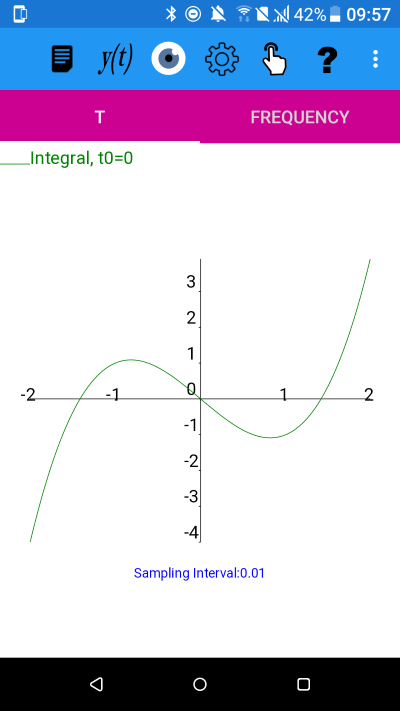
The integral, with t0=0, of the derivative of y(t)=t^3-2*t+1
Plot after saving derivative values to a file, reading them back in again and displaying only the integral with initial value t0=0.
The two graphs differ by a shift downwards in the y direction (i.e. by a constant value).
Why do the graphs differ?
We are solving the differential equation:
df/dt=y'
and this gives:
f=y+C where C is the constant of integration.
plotXpose performs numerical integration by assuming that the integral is zero at some initial value, and in the graph above we have used t0=0. This is equivalent to the initial condition that f=0 at t=0. This initial condition, we have shown, is not consistent with our original function - as the two graphs above differ.
To get back the original function of t^3-2*t+1 we need to use a correct initial condition. As plotXpose calculates the integral with reference to a value of t where the integral is 0 then we need to use a value of t^3-2*t+1 where the function is zero for our initial condition.
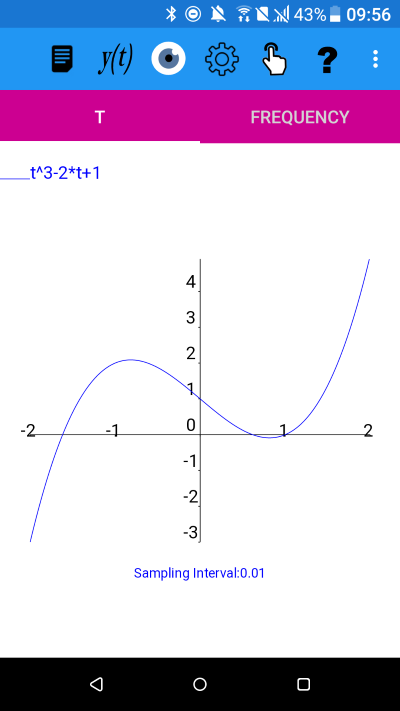
We can possibly solve t^3-2*t+1=0 by using a guess. From the graph of t^3-2*t+1 it appears that t=1 is a zero. Substituting t=1 in y= t^3-2*t+1 we get y =1-2+1=0. Hence t=1 is a solution to t^3-2*t+1=0.
We now know that we need to solve df/dt=y' where f=0 when t=1, so we change the integration to use t0=1.
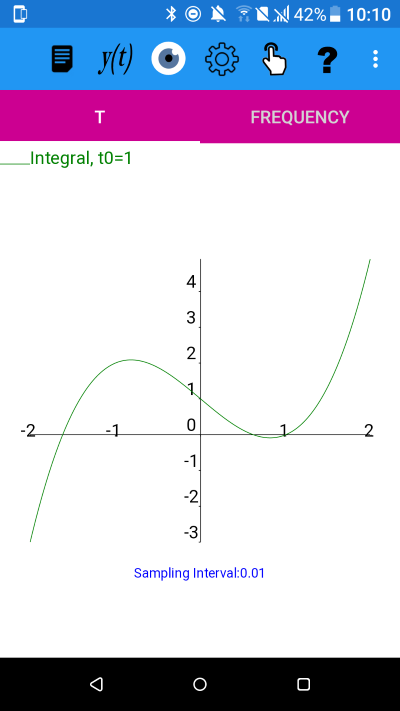
The integral, with t0=1, of the derivative of y(t)=t^3-2*t+1
Plot after saving derivative values to a file, reading them back in again and displaying only the integral with initial value t0=1.
The two plots now appear to be the same
Conclusion
We have shown that integration can be inverse differentiation, if the correct initial value is chosen.Note: As y(t)=t^3-2*t+1 is a cubic function it will have 3 roots and, in this case, from the graph, we can see that they are all the roots are real as the function crosses the t axis in three places. We can find the other two roots by dividing t^3-2*t+1 by the know factor of (t-1) and then solving the resulting quadratic, or we can use Newton-Raphson to solve numerically for the other two roots.
The other two roots, to 8 significant figures, are -1.618034 and 0.61803399. Using either of these values for t0 when integrating the derivative, will also result in the initial function (to within rounding errors).
The other two roots, to 8 significant figures, are -1.618034 and 0.61803399. Using either of these values for t0 when integrating the derivative, will also result in the initial function (to within rounding errors).
plotXpose app is available on Google Play and App Store
Google Play and the Google Play logo are trademarks of Google LLC.
A version will shortly be available for Windows.
A version will shortly be available for Windows.
plotXpose app is a companion to the book Mathematics for Electrical Engineering and Computing by Mary Attenborough, published by Newnes, 2003.