Is this a fix? - Solution
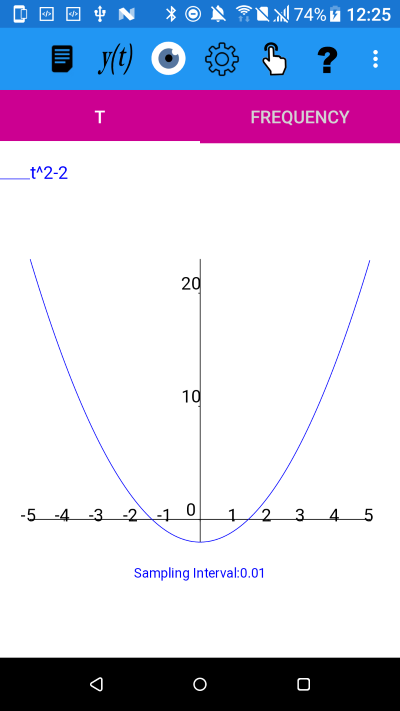
The graph of y(t)=t^2-2
Solving t^2-2=0: Success. The Fix point method, using function 1+1/(t+1) has converged to the value (1.4142135623731,4.44089209850063E-016).
The sequence of values found was
( n, t , y(t))
(0, 0.653594791889191, -1.572813848015326E+000)
(1, 1.60474307545292, 5.752003382140951E-001)
(2, 1.38391502387471, -8.477920669385353E-002)
(3, 1.41947803926947, 1.491790396830339E-002)
(4, 1.41331228627392, -2.548381467192717E-003)
(5, 1.41436825465467, 4.375597749040061E-004)
(6, 1.41418702307409, -7.506376884935939E-005)
(7, 1.41421811584699, 1.287918980796832E-005)
(8, 1.41421278112196, -2.209711290612759E-006)
(9, 1.41421369641464, 3.791267650932184E-007)
(10, 1.4142135393752, -6.504786154160058E-008)
(11, 1.41421356631891, 1.116044856530607E-008)
(12, 1.4142135616961, -1.914829850235833E-009)
(13, 1.41421356248925, 3.285327565549778E-010)
(14, 1.41421356235317, -5.636735522784875E-011)
(15, 1.41421356237651, 9.671374812114664E-012)
(16, 1.41421356237251, -1.659561377209684E-012)
(17, 1.4142135623732, 2.846611835138901E-013)
(18, 1.41421356237308, -4.862776847858186E-014)
(19, 1.4142135623731, 8.437694987151190E-015)
(20, 1.41421356237309, -1.554312234475219E-015)
(21, 1.4142135623731, 4.440892098500626E-016)
The sequence of values found was
( n, t , y(t))
(0, 0.653594791889191, -1.572813848015326E+000)
(1, 1.60474307545292, 5.752003382140951E-001)
(2, 1.38391502387471, -8.477920669385353E-002)
(3, 1.41947803926947, 1.491790396830339E-002)
(4, 1.41331228627392, -2.548381467192717E-003)
(5, 1.41436825465467, 4.375597749040061E-004)
(6, 1.41418702307409, -7.506376884935939E-005)
(7, 1.41421811584699, 1.287918980796832E-005)
(8, 1.41421278112196, -2.209711290612759E-006)
(9, 1.41421369641464, 3.791267650932184E-007)
(10, 1.4142135393752, -6.504786154160058E-008)
(11, 1.41421356631891, 1.116044856530607E-008)
(12, 1.4142135616961, -1.914829850235833E-009)
(13, 1.41421356248925, 3.285327565549778E-010)
(14, 1.41421356235317, -5.636735522784875E-011)
(15, 1.41421356237651, 9.671374812114664E-012)
(16, 1.41421356237251, -1.659561377209684E-012)
(17, 1.4142135623732, 2.846611835138901E-013)
(18, 1.41421356237308, -4.862776847858186E-014)
(19, 1.4142135623731, 8.437694987151190E-015)
(20, 1.41421356237309, -1.554312234475219E-015)
(21, 1.4142135623731, 4.440892098500626E-016)
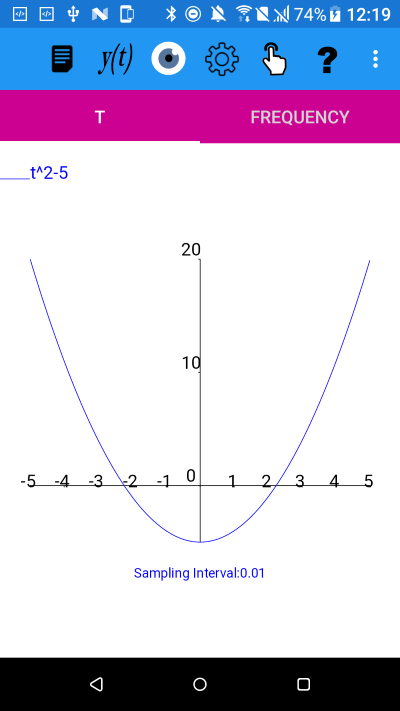
The graph of y(t)=t^2-5
To find a suitable fix point function to find the square root of 5 using a Fix point method, we can begin with:
t^2= 5
subtract the square of an integer from both sides (in this case 4) gives:
t^2-4=1
use the difference of two squares factorization on the left-hand-side to get
(t-2)(t+2)=1
divide by one of the factors on the left-hand-side giving (t-2)=1/(t+2)
and finally add 2 to both sides giving
t=2+1/(t+2)
i.e. the fix point function to use is fix(t)=2+1/(t+2).
Solving t^2-5=0: Success. The Fix point method, using function 2+1/(t+2) has converged to the value (2.2360679774998,8.88178419700125E-016).
The sequence of values found was
( n, t , y(t))
(0, 1.45969498157501, -2.869290560764725E+000)
(1, 2.28904282178794, 2.397170399788733E-001)
(2, 2.23315225367303, -1.303101191505629E-002)
(3, 2.23623057713842, 7.271941288475858E-004)
(4, 2.2360589164803, -4.052202895898915E-005)
(5, 2.23606848245418, 2.258224937712328E-006)
(6, 2.23606794935965, -1.258465323061841E-007)
(7, 2.23606797906799, 7.013187364179885E-009)
(8, 2.2360679774124, -3.908322554480037E-010)
(9, 2.23606797750466, 2.178168756472587E-011)
(10, 2.23606797749952, -1.215028078149771E-012)
(11, 2.2360679774998, 6.838973831690964E-014)
(12, 2.23606797749979, -3.552713678800501E-015)
(13, 2.23606797749979, 8.881784197001252E-016)
(14, 2.23606797749979, 8.881784197001252E-016)
The sequence of values found was
( n, t , y(t))
(0, 1.45969498157501, -2.869290560764725E+000)
(1, 2.28904282178794, 2.397170399788733E-001)
(2, 2.23315225367303, -1.303101191505629E-002)
(3, 2.23623057713842, 7.271941288475858E-004)
(4, 2.2360589164803, -4.052202895898915E-005)
(5, 2.23606848245418, 2.258224937712328E-006)
(6, 2.23606794935965, -1.258465323061841E-007)
(7, 2.23606797906799, 7.013187364179885E-009)
(8, 2.2360679774124, -3.908322554480037E-010)
(9, 2.23606797750466, 2.178168756472587E-011)
(10, 2.23606797749952, -1.215028078149771E-012)
(11, 2.2360679774998, 6.838973831690964E-014)
(12, 2.23606797749979, -3.552713678800501E-015)
(13, 2.23606797749979, 8.881784197001252E-016)
(14, 2.23606797749979, 8.881784197001252E-016)
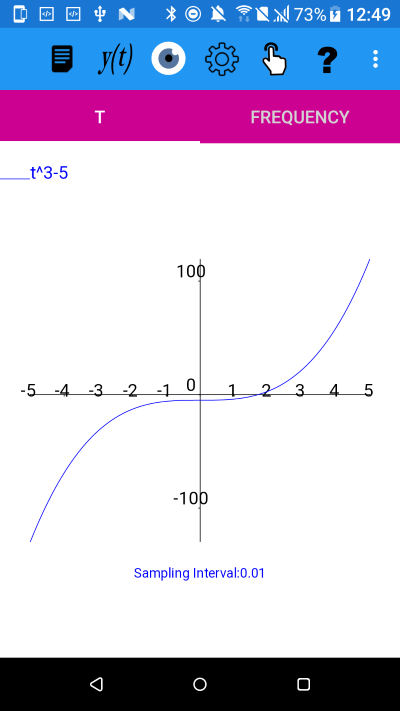
The graph of y(t)=t^3-5
To find a suitable fix point function to find the cubed root of 5, using a Fix point method, we can begin with:
t^3=5
In order to use the well-known factorisation of the difference of two cubes, we subtract an integer cube from both sides, in this case 1, giving
t^3-1=4
Factorise to give:
(t-1)(t^2+t+1)=4
Divide both sides by (t^2+t+1)
t-1 = 4/(t^2+t+1)
Finally add 1 to both sides to give
t =1+4/(t^2+t+1)
So fix(t)=1+4/(t^2+t+1)
To use this fix point function we increase the potential number of iterations to the maximum of 100, giving e.g. the result below.
Solving t^3-5=0: Success. The Fix point method, using function 1+4/(t^2+t+1) has converged to the value (1.7099759466767,1.06581410364015E-014).
The sequence of values found was
( n, t , y(t))
(0, 0.816993474960327, -4.454674553072264E+000)
(1, 2.61000015332361, 1.277958413336753E+001)
(2, 1.38379977489955, -2.350159296664016E+000)
(3, 1.93051353169673, 2.194797089695588E+000)
(4, 1.60083551937128, -8.975798598007518E-001)
(5, 1.77466686292552, 5.892111959473372E-001)
(6, 1.67520698425003, -2.988357491481857E-001)
(7, 1.72972387982472, 1.752381954589346E-001)
(8, 1.69909676589793, -9.482687965940073E-002)
(9, 1.71607249599932, 5.367015039466594E-002)
(10, 1.70659177430073, -2.962742779927474E-002)
(11, 1.71186445246782, 1.658437568343985E-002)
(12, 1.70892518208005, -9.211700132656375E-003)
(13, 1.71056155206591, 5.138721062757590E-003)
(14, 1.70964987887097, -2.859738763023145E-003)
(15, 1.71015759517167, 1.593599538222357E-003)
(16, 1.70987478114081, -8.873769632460338E-004)
(17, 1.71003229771685, 4.943306128728509E-004)
(18, 1.70994456088438, -2.753127871137906E-004)
(19, 1.70999342845178, 1.533526291108700E-004)
(20, 1.70996620965557, -8.541318107102569E-005)
(21, 1.70998137009741, 4.757468594629444E-005)
(22, 1.70997292591266, -2.649825607115020E-005)
(23, 1.70997762920492, 1.475924159244357E-005)
(24, 1.70997500953174, -8.220680901338540E-006)
(25, 1.70997646865424, 4.578816199085622E-006)
(26, 1.70997565594223, -2.550337751650034E-006)
(27, 1.70997610861195, 1.420504805338396E-006)
(28, 1.70997585648092, -7.912020905109785E-007)
(29, 1.70997599691455, 4.406890958819076E-007)
(30, 1.70997591869488, -2.454579473010199E-007)
(31, 1.70997596226219, 1.367168174226663E-007)
(32, 1.70997593799578, -7.614944852463168E-008)
(33, 1.70997595151185, 4.241422946194007E-008)
(34, 1.70997594398358, -2.362415951751018E-008)
(35, 1.70997594817673, 1.315834197157528E-008)
(36, 1.7099759458412, -7.329021833868410E-009)
(37, 1.70997594714206, 4.082166604746362E-009)
(38, 1.7099759464175, -2.273713661793408E-009)
(39, 1.70997594682107, 1.266428739654657E-009)
(40, 1.70997594659628, -7.053824191416425E-010)
(41, 1.70997594672149, 3.928883884896095E-010)
(42, 1.70997594665175, -2.188329517593957E-010)
(43, 1.70997594669059, 1.218873890707073E-010)
(44, 1.70997594666896, -6.788969386661847E-011)
(45, 1.70997594668101, 3.781508439715253E-011)
(46, 1.7099759466743, -2.106315122318847E-011)
(47, 1.70997594667803, 1.173194874581895E-011)
(48, 1.70997594667595, -6.536104990573222E-012)
(49, 1.70997594667711, 3.641531520770514E-012)
(50, 1.70997594667647, -2.028599510595086E-012)
(51, 1.70997594667683, 1.129762949858559E-012)
(52, 1.70997594667663, -6.306066779870889E-013)
(53, 1.70997594667674, 3.517186542012496E-013)
(54, 1.70997594667667, -1.945110739143274E-013)
(55, 1.70997594667671, 1.074695887837152E-013)
(56, 1.70997594667669, -5.950795411990839E-014)
(57, 1.7099759466767, 3.375077994860476E-014)
(58, 1.70997594667669, -1.865174681370263E-014)
(59, 1.7099759466767, 1.065814103640150E-014)
The sequence of values found was
( n, t , y(t))
(0, 0.816993474960327, -4.454674553072264E+000)
(1, 2.61000015332361, 1.277958413336753E+001)
(2, 1.38379977489955, -2.350159296664016E+000)
(3, 1.93051353169673, 2.194797089695588E+000)
(4, 1.60083551937128, -8.975798598007518E-001)
(5, 1.77466686292552, 5.892111959473372E-001)
(6, 1.67520698425003, -2.988357491481857E-001)
(7, 1.72972387982472, 1.752381954589346E-001)
(8, 1.69909676589793, -9.482687965940073E-002)
(9, 1.71607249599932, 5.367015039466594E-002)
(10, 1.70659177430073, -2.962742779927474E-002)
(11, 1.71186445246782, 1.658437568343985E-002)
(12, 1.70892518208005, -9.211700132656375E-003)
(13, 1.71056155206591, 5.138721062757590E-003)
(14, 1.70964987887097, -2.859738763023145E-003)
(15, 1.71015759517167, 1.593599538222357E-003)
(16, 1.70987478114081, -8.873769632460338E-004)
(17, 1.71003229771685, 4.943306128728509E-004)
(18, 1.70994456088438, -2.753127871137906E-004)
(19, 1.70999342845178, 1.533526291108700E-004)
(20, 1.70996620965557, -8.541318107102569E-005)
(21, 1.70998137009741, 4.757468594629444E-005)
(22, 1.70997292591266, -2.649825607115020E-005)
(23, 1.70997762920492, 1.475924159244357E-005)
(24, 1.70997500953174, -8.220680901338540E-006)
(25, 1.70997646865424, 4.578816199085622E-006)
(26, 1.70997565594223, -2.550337751650034E-006)
(27, 1.70997610861195, 1.420504805338396E-006)
(28, 1.70997585648092, -7.912020905109785E-007)
(29, 1.70997599691455, 4.406890958819076E-007)
(30, 1.70997591869488, -2.454579473010199E-007)
(31, 1.70997596226219, 1.367168174226663E-007)
(32, 1.70997593799578, -7.614944852463168E-008)
(33, 1.70997595151185, 4.241422946194007E-008)
(34, 1.70997594398358, -2.362415951751018E-008)
(35, 1.70997594817673, 1.315834197157528E-008)
(36, 1.7099759458412, -7.329021833868410E-009)
(37, 1.70997594714206, 4.082166604746362E-009)
(38, 1.7099759464175, -2.273713661793408E-009)
(39, 1.70997594682107, 1.266428739654657E-009)
(40, 1.70997594659628, -7.053824191416425E-010)
(41, 1.70997594672149, 3.928883884896095E-010)
(42, 1.70997594665175, -2.188329517593957E-010)
(43, 1.70997594669059, 1.218873890707073E-010)
(44, 1.70997594666896, -6.788969386661847E-011)
(45, 1.70997594668101, 3.781508439715253E-011)
(46, 1.7099759466743, -2.106315122318847E-011)
(47, 1.70997594667803, 1.173194874581895E-011)
(48, 1.70997594667595, -6.536104990573222E-012)
(49, 1.70997594667711, 3.641531520770514E-012)
(50, 1.70997594667647, -2.028599510595086E-012)
(51, 1.70997594667683, 1.129762949858559E-012)
(52, 1.70997594667663, -6.306066779870889E-013)
(53, 1.70997594667674, 3.517186542012496E-013)
(54, 1.70997594667667, -1.945110739143274E-013)
(55, 1.70997594667671, 1.074695887837152E-013)
(56, 1.70997594667669, -5.950795411990839E-014)
(57, 1.7099759466767, 3.375077994860476E-014)
(58, 1.70997594667669, -1.865174681370263E-014)
(59, 1.7099759466767, 1.065814103640150E-014)
plotXpose app is available on Google Play and App Store
Google Play and the Google Play logo are trademarks of Google LLC.
A version will shortly be available for Windows.
A version will shortly be available for Windows.
plotXpose app is a companion to the book Mathematics for Electrical Engineering and Computing by Mary Attenborough, published by Newnes, 2003.