Maximum value - Solution

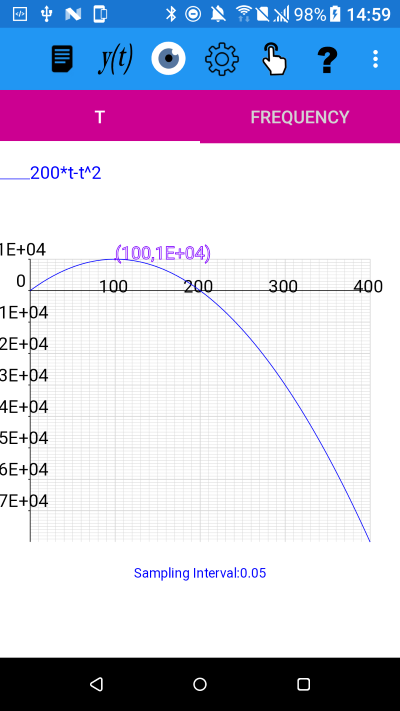
y(t)=200*t-t^2 for 0<=t<400 with a sampling interval of 0.05.

t represents the length of one side of a rectangular field with a perimeter of 400 and y represents the area of the field.

y(t)=200*t-t^2 for 0<=t<400 with a sampling interval of 0.05 displaying the derivative.

y(t)=200*t-t^2 displaying the derivative. t represents the length of one side of a rectangular field with a perimeter of 400 and y represents the area of the field. Mathematics for Electrical Engineering and Computing plotXpose app problem

We have used the view menu to set the display of the derivate on and Settings -> y-axis to set the y-axis range to -1000 <=y <=1000

From the graph we can see that the maximum value for y seems to be at t=100 and using 'Display Position' from the mode menu we can input t=100 to get the following result:

Values for 200*t-t^2:

Function: (100, 10000)
Derivative: (100, 0)

This confirms that the maximum does occur at t=100, where we have found that the derivative is 0.

The maximum area of a field of perimeter 400 is 10000 and, to obtain this area, the length of the side should be 100, i.e. the field should be a square of side 100.

plotXpose app is available on Google Play

Google Play and the Google Play logo are trademarks of Google LLC.
Versions will shortly be available for iOS and Windows.

plotXpose app is a companion to the book Mathematics for Electrical Engineering and Computing by Mary Attenborough, published by Newnes, 2003.