The biased integral - Solution
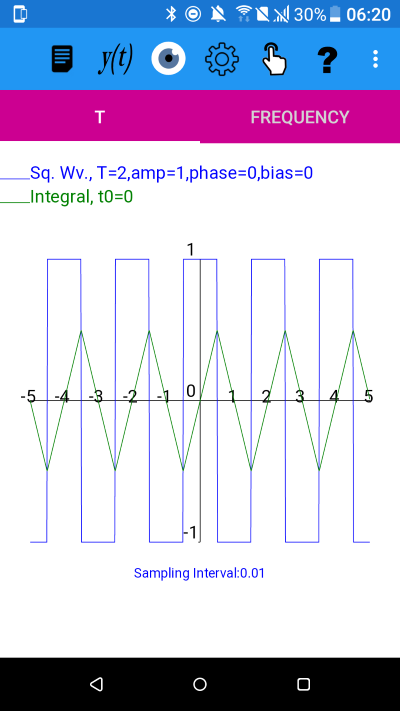
An unbiased square wave showing its integral which is a triangular wave
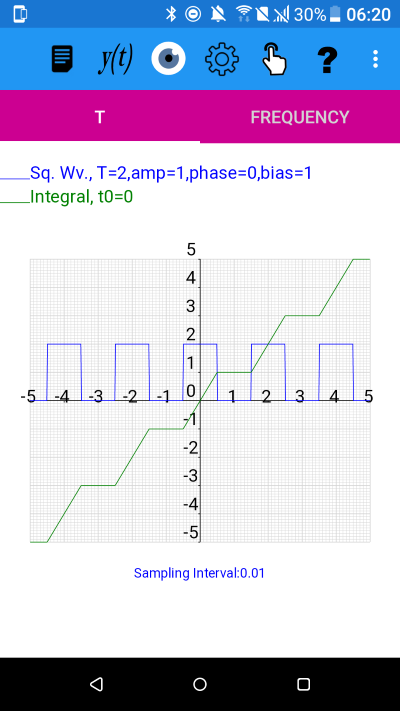
A square wave with an offset of 1 showing a sloping integral
From the graph we can see that the integral is 5 when t=5 and 0 when t=0. The slope is given by:
increase in y / increase in t (as long as we choose points of the same phase), and from t=0 to t=5 this gives 5/5 =1.
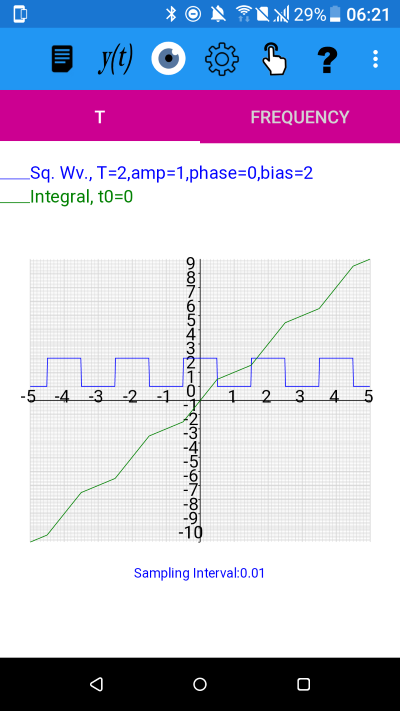
A square wave with an offset of 2 showing a sloping integral
From the graph we can see that the integral is 10 when t=5 and 0 when t=0. Choosing points in the same phase, the slope is given by:
(increase in y)/ (increase in t)
At t=0 the integral has value and at t=5 the integral is 10
Slope = (10-0)/(5-0) =2
From these examples we could surmise that the additional slope of the graph of the integral is equal to the offset of the square wave.
The general case - The Integral of a Square Wave
The square wave with amplitude 1, period 2, 0 phase and 0 offset can be defined as a periodic function such that:
y(t)= 1 (|t|<0.5)
y(t)= -1 (|t|>0.5)
y(t)=0 (|t|=0.5)
The definition is then repeated periodically with y(t+2) = y(t)
And for a square wave of amplitude 1, period p and zero phase and zero offset it can be defined, over the cycle where |t|<p/2 as:
y(t)= 1 (|t|<p/4)
y(t)= -1 (|t|>p/4)
y(t)=0 (|t|=p/4)
The definition is then repeated periodically with y(t+p) = y(t)
We consider the integral over one complete period from -p/2 to p/2
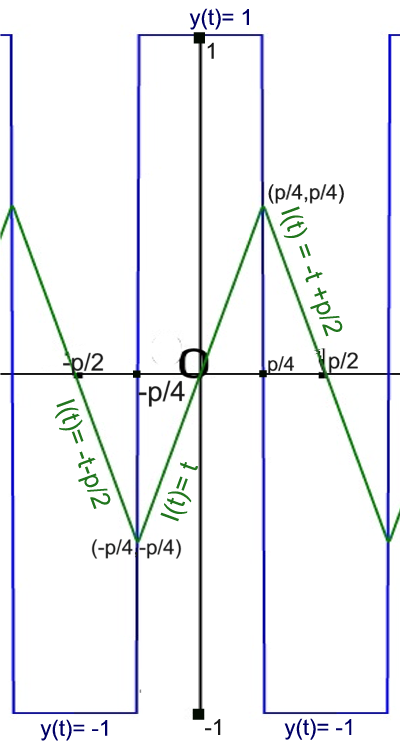
To show that this is a triangular wave we perform the integration in sections
Section 1 - Integrating y from -p/2 to t where -p/2<t<-p/4
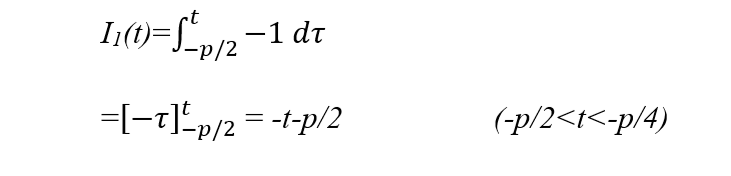
Section 2 - Integrating y from -p/4 to t where t<p/4
We need to consider the integral so far i.e. up to -p/4, which is given by:
I1(-p/4) = -(p/4)-p/2 = -p/4
We start from this initial value and then integrate over Section 2
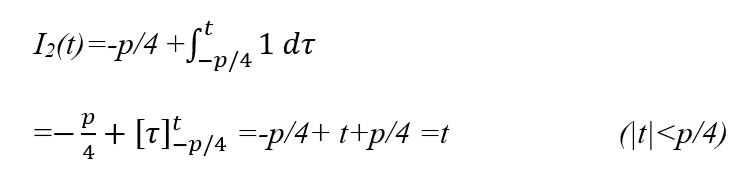
Section 3 Integrating y from p/4 to t where p/4<t<p/2
We need to consider the integral so far - up to p/4, which is given by:
I2(p/4) = p/4
We start from this initial value and then integrate over Section 3
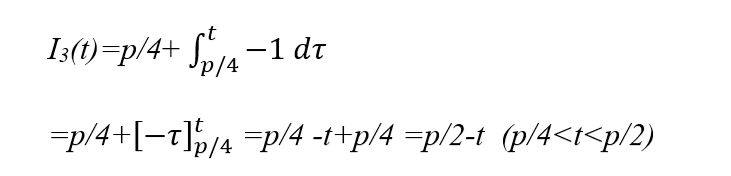
Putting these sections together we have:
I(t)= -t-p/2 (-p/2<t<-p/4)
I(t)= t (|t|<p/4)
I(t) = p/2-t (p/4<t<p/2)
This is a triangular wave - see Figure below.
Adding an offset ,c, to the original function adds a constant value,c, to the original function.
c, integrated with respect to time, is ct so the addition of c to the function adds ct to the integral. y=ct describes a line with slope c.
As c is the offset then the additional slope of the integral of a biased square wave will be c due to the offset.
plotXpose app is available on Google Play and App Store
Google Play and the Google Play logo are trademarks of Google LLC.
A version will shortly be available for Windows.
A version will shortly be available for Windows.
plotXpose app is a companion to the book Mathematics for Electrical Engineering and Computing by Mary Attenborough, published by Newnes, 2003.