There's nothing like a zero? - Solution

Enter the function y(t)=(1-t)^6

Click on y(t) in the menu and then on the submenu (...) and select 'General'
Enter the function as above and click OK.

Change the View settings so that the derivative is not shown

Select the View Icon and from the View window turn off the display Derivative switch.

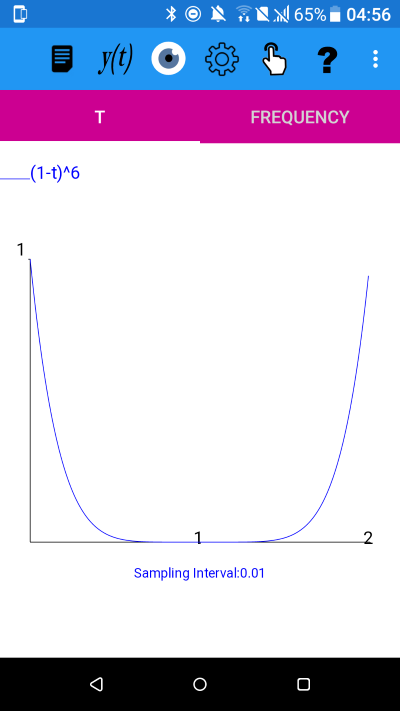
Change the t-axis and the Sample interval

Click on the settings icon and then the submenu (...) and select 't-axis' and change the range to 0 to 2. After selecting OK then select 'Sample Interval' from the submenu and change the value to 0.001 and press OK.

The graph plotted with plotXpose for 0<=t<=2 with a sampling interval 0.001 is

Perform Zero Finding

Now click on the Mode icon and then the submenu (...) and select 'Zero Find'. Change the Accuracy value (No. of significant figures) to 10 and the Maximum no. of iterations to 100 and press OK.
Click on the t axis near the point t=1.

An example of the output for Newton-Raphson is:



We see that plotXpose has reported a failure to converge to the required accuracy.

This sequence will be saved to your clipboard so if you want to save the sequence that you obtained then simply paste it into a document.

Newton-Raphson method for solving equations

Pages 283 to 286 of Mathematics for Electrical Engineering and Computing explains the Newton-Raphson method for solving equations, which can be expressed using the following algorithm:

1. Write the equation in the form f(t)=0
   
2. Take a guess at the solution, t0.
   
3. Calculate tnplus1= tn - f(tn)/f'(tn) until some convergence criterion is satisfied.

Applying Newton-Raphson where f(t) = (1-t)^6

Considering our function f(t) = (1-t)^6, where we want to find a solution to the equation f(t)=0, then f'(t) = -6*(1-t)^5. Step (3) of the Newton Raphson algorithm gives us tnplus1= tn + (1-tn)^6)/(6*(1-tn)^5 , which simplifies to tnplus1= tn + (1-tn)/6 for tn!=1. i.e

Convergence of Newton-Raphson

Usually, providing a suitable starting value is chosen, Newton-Raphson converges quadratically, i.e. the relative error, between the current approximation and the root, is squared at each step, resulting in the number of accurate digits roughly doubling.

Convergence of Newton-Raphson where f(t) = (1-t)^6

We can see that the expression (1) in this case will converge only linearly, because the recurrence relation obtained is a linear function.

Even with such a slower convergence rate we might expect that plotXpose would converge to the required root. However plotXpose has ceased the calculation before reaching the required accuracy and reported that the derivative is too small. This result is because the plotXpose app does not perform symbolic manipulations, so the simplification that we were able to do in Step (3) above has not been used. plotXpose is calculating tnplus1= tn - f(tn)/f'(tn) i.e.

The derivative in the denominator of the second term on the right hand side of the recurrence relation will become smaller than the precision of a double floating-point number, as tn approaches the root of 1. In our example this has happened before we reached the desired level of accuracy for the root, and the value found by plotXpose after 28 iterations is only accurate to 3 significant figures.

The problem of Root Multiplicity

The function we have considered has 6 repeated roots at t=1. The problem we have encountered here may occur wherever there is root multiplicity, i.e. repeated roots. Similar numerical issues can be encountered were a function has roots that are very close together. In such cases alternative, more advanced numerical methods for root finding - beyond the scope of our considerations, may provide a more suitable numerical approach to zero finding.

---