The root of the problem - Solution

Enter the function y(t)=t^2-2049

Tap on y(t) in the menu and then on the submenu (⋮) and select 'General'
Enter the function as above and click OK.

Change the View settings so that the derivative is not shown

Select the View Icon and from the View window turn off the display Derivative switch.

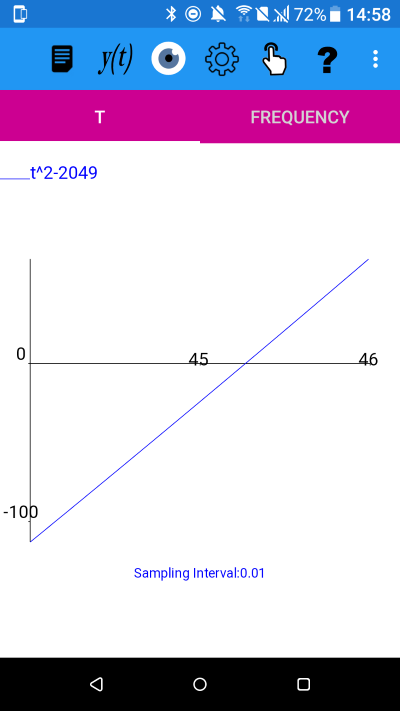
Change the t-axis

Tap on the settings icon and then the submenu (⋮) and select 't-axis' and change the range to 44 to 46 and tap on OK.

y(t)=t^2-2049 with 44<=t<46

Tap on the 'Mode' icon and then on the submenu (⋮) and select 'Zero Find'. Change the Accuracy (No. of s.f.) to 14 and tap OK. You will get the message popup "Click on the t-axis" and after tapping OK on this popup then click once on the t-axis in the vicinity of where the graph crosses the t-axis. After performing the zero-finding plotXpose will display the result and the sequence of values found during the calculation. An example output is below, where Newton- has calculated the square root of 2049 as 45.265881191025 to 14 significant figures.

Solving t^2-2049=0: Success. The Newton-Raphson method has converged to the value (45.265881191025,0.00000000000000E+000).
The sequence of values found was
( n, t , y(t))
(0, 44.9651412963867, -2.713606819597771E+001)
(1, 45.2668869088058, 9.105041461407382E-002)
(2, 45.2658812021974, 1.011445874610217E-006)
(3, 45.2658811910251, 0.000000000000000E+000)
(4, 45.2658811910251, 0.000000000000000E+000)
(5, 45.2658811910251, 0.000000000000000E+000)

plotXpose app is available on Google Play and App Store

Google Play and the Google Play logo are trademarks of Google LLC.
A version will shortly be available for Windows.

plotXpose app is a companion to the book Mathematics for Electrical Engineering and Computing by Mary Attenborough, published by Newnes, 2003.